
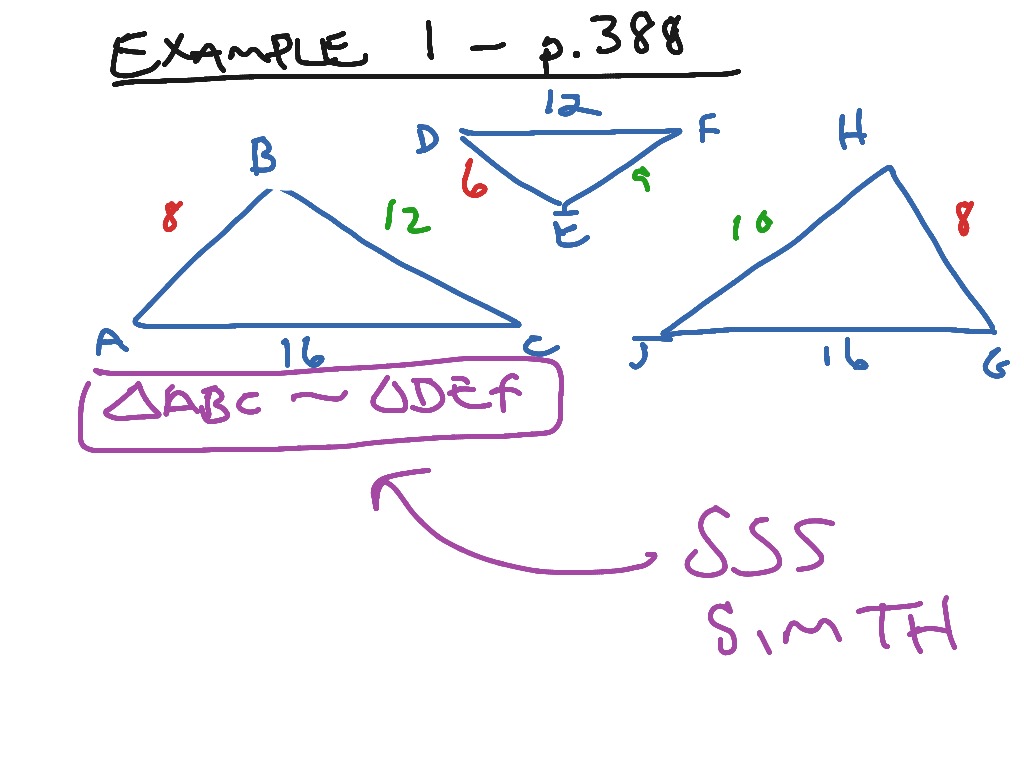
If all three sides in one triangle are the same. There are five ways to test that two triangles are congruent. Lining up the corresponding sides, we have A B C L M K. Congruent Triangles - Three sides equal (SSS) Definition: Triangles are congruent if all three sides in one triangle are congruent to the corresponding sides in the other. From the SSS Postulate, the triangles are congruent. (2) \(SAS = SAS\): \(AC\), \(\angle C\), \(BC\) of \(\triangle ABC = EC\), \(\angle C\), \(DC\) of \(\triangle EDC\). Write a triangle congruence statement based on the picture below: From the tic marks, we know ¯ A B ¯ L M, ¯ A C ¯ L K, ¯ B C ¯ M K. (1) \(\triangle ABC \cong \triangle EDC\). (3) \(AB = ED\) ecause they are corresponding sides of congruent triangles, Since \(ED = 110\), \(AB = 110\). Sides \(AC\), \(BC\), and included angle \(C\) of \(ABC\) are equal respectively to \(EC, DC\), and included angle \(C\) of \(\angle EDC\). Therefore the "\(C\)'s" correspond, \(AC = EC\) so \(A\) must correspond to \(E\). The teachers took informed risks in telling their stories, like Trisha who. (1) \(\angle ACB = \angle ECD\) because vertical angles are equal. SSS stands for 'side, side, side' and means that we have two triangles with all three sides equal. Another similar example was Coles (2008) unpublished doctoral dissertation. This is because interior angles of triangles add to 180. This forces the remaining angle on our CAT to be: 180-\angle C-\angle A 180 C A. The two triangles have two angles congruent (equal) and the included side between those angles congruent. Then \(AC\) was extended to \(E\) so that \(AC = CE\) and \(BC\) was extended to \(D\) so that \(BC = CD\). The detection of local shape changes via the geometry of Hotellings T2 elds, Annals of. It is equal in length to the included side between B and U on BUG. (SSS, SAS, ASA, AAS, HL) If not, state that it is not sufficient to prove that the triangles are congruent. The following procedure was used to measure the d.istance AB across a pond: From a point \(C\), \(AC\) and \(BC\) were measured and found to be 80 and 100 feet respectively. Example 1: If they pairs of triangles below are congruent, then name their congruence criteria. Geometry Teachers Never Spend Time Trying to Find Materials for Your Lessons AgainJoin Our Geometry Teacher Community Today. x y 1 1 A(24, 21) F(0, 3) D(4, 1) E(2, 0) C(0, 23) B(22, 0) ExamPlE 2 Study guide continued For use with the lesson Prove Triangles Congruent by SSS Geometry 4-54 Chapter Resource Book Lesson 4.4 Lesson 4. \(AC\), \(\angle ACB\), \(BC\) of \(\triangle ABC\) = \(EC, \angle ECD, DC\) of \(\triangle EDC\). So, by the SSS Congruence Postulate, you know that n ABC > nCDE.\), the shape of \(\triangle ABC\) cannot be changed as long as the lengths of its sides remain the same.\]


 0 kommentar(er)
0 kommentar(er)
